Pipelines Part 2: Categorical Pipelines
In the previous post we saw how to implement pipelines and their benefits:
- Separate the specification of the pipeline from its implementation
- Provide multiple runtimes for the same pipeline
We are now going to generalise the pipeline architecture to categories so that Run and RunM will be one and the same.
In addition to handling effects, this makes the pipeline able to compute any sequence of morphisms in any category, and we are
going to see how to use the same infrastructure to build a pipeline in the category of dependent lenses. Finally, the
pipeline architecture can be further generalised to graded categories providing the same benefit but for graded morphisms,
and we are going to use this functionality to automatically combine errors in effectful programs.
Abstracting to categories
You might have noticed that Run and RunM share many similarities:
Run [x, y] f = f
Run (x :: y :: z :: xs) (f, cont) = Run (y :: z :: xs) cont . f
RunM [x, y] f = f
RunM (s :: t :: x :: xs) (f, cont) = RunM (y :: z :: xs) cont <=< f
The base case is the same and the inductive case differs only in how we compose functions, in the simple case we use function composition (.) and in the monadic case we use kleisli composition <=<. Can we abstract over what composition operator we use? We sure can. In fact, doing so means that we’re abstracting over categories. That is, we are going to abstract over a generic composition operator (.) : arr b c -> arr a b -> arr a c with a generic “arrow type”arr : o -> o -> Type . This is the basic definition of a category as an interface in idris:
-- "| arr" means that the 'arr' argument is uniquely defined
-- for each instance of this interface, but `obj` isn't.
interface Category (0 arr : obj -> obj -> Type) | arr where
id : arr a a
(.) : arr b c -> arr a b -> arr a c
To use this in our generalisation, we need to change our definition of pipeline to not be about types but to be about objects in a category. We represent this using parameter blocks:
parameters (o : Type) (arr : o -> o -> Type)
We simplify our definition of ImplCat using higher order functions instead of pattern matching.
ImplCat : Vect (2 + n) o -> Type
ImplCat = All (uncurry arr) . pairUp
We implement RunCat in the same way as before except (.) now refers to
the composition of morphism of the Category interface.
RunCat : Category arr =>
(p : Vect (2 + n) o) ->
ImplCat p -> arr (head p) (last p)
RunCat [x, y] [f] = f
RunCat (x :: y :: z :: xs) (f :: cont) = RunCat (y :: z :: xs) cont . f
With this setup we can now use the same code for both pure and effecful pipelines! The only difference between the two is what category is used to run the pipeline. In the pure case, we use plain functions where objects are Type and arrows are Fn. In the effectful case we use Kleisli Morphisms where the objects are type and the morphisms are given by Kleisli m where m : Type -> Type is a monad, it defines the class of functions a -> m b.
Remember that we had two compiler definitions, a pure one without side effects:
lex : List Char -> List Token
parse : List Token -> Tree
typecheck : Tree -> Sema
codegen : Sema -> Bytecode
And a monadic one where errors are handled using the Maybe monad.
lexM : List Char -> Maybe (List Token)
parseM : List Token -> Maybe Tree
typecheckM : Tree -> Maybe Sema
codegenM : Sema -> Maybe Bytecode
Using the same RunCat we can execute the pipeline CompilerPipeline in those two different categories. First one where objects are Type and morphisms are functions, and the second one where objects are also Type and the morphisms are kleisli morphisms, represented by the KleisliMorphism type.
CompilerPipeline : Vect ? Type
CompilerPipeline = [String, List Char, List Token, Tree, Sema, Bytecode]
runCompiler' : String -> Bytecode
runCompiler' =
RunCat Type Fn CompilerPipeline
[unpack, lex, parse, typecheck, codegen]
Here you can see that the first two arguments are the objects and morphisms of the category we are working on and the pipeline and implementation are the same as before.
-- equivalent to String -> Maybe Bytecode
runCompilerM' : Kleislimorphism Maybe String Bytecode
runCompilerM' =
RunCat Type (Kleislimorphism Maybe) CompilerPipeline
[Kleisli (pure . unpack),
Kleisli lexM,
Kleisli parseM,
Kleisli typecheckM,
Kleisli codegenM]
Likewise, the first two arguments are the object and morphisms: in this case, the morphisms are Kleislimorphism Maybe which is equivalent to a newtype around x -> Maybe y. Because Kleislimorphism is a newtype, we need to wrap each value around its constructor Kleisli.
Pipelines of lenses
Because lenses form a category, we can define a pipeline as a list of input-output pairs where the morphisms between each layer are lenses. In our case we can do even better and use dependent lenses/container morphisms as our category, and build entire applications with them.
For example, the following program describes a command-line program written using containers and stages between them to communicate with a database.
The first stage converts from an effectful CLI interface that receives and sends strings into an abstract type of messages that the app
can deal with. The internal API of the app exposing those messages is given by the AppOp container. After distributing the monads around, each
of those messages is converted into a database query. Database queries are then executed by the database and the result is returned to the client.
This entire pipeline is represented as a list of containers, where FM is the effectful comonad on container, MaybeAll the Maybe monad on
containers and CUnit the monoidal unit.
0 AppPipeline : Vect 6 Container
AppPipeline = [ FM CLI
, FM (MaybeAll AppOp)
, MaybeAll (FM AppOp)
, MaybeAll (FM DB_API)
, MaybeAll CUnit
, CUnit
]
The implementation is given by a sequence of morphisms with the right domain and codomain.
appImpl : DB => ImplCat Container (=%>) AppPipeline
appImpl = [ parser
, distribMaybeAF {a = AppOp}
, map_MaybeAll (mapLift' OpToDB)
, map_MaybeAll DBCostate
, maybeAUnit
]
This pipeline can also be represented graphically:
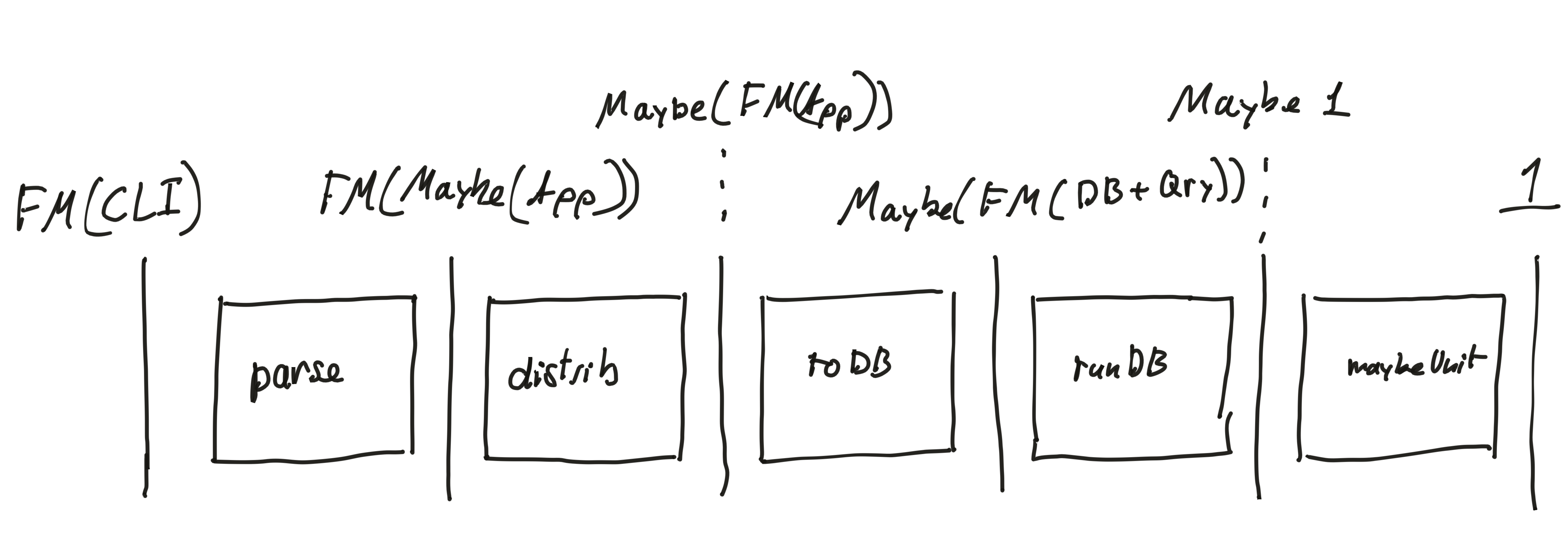
Unfortunately we cannot use kleisli morphisms with this pipeline because we are not using the same monad across the entire pipeline.
The problem of dealing with different monads appears much earlier, if we write a pipeline where each morphism is a different coproduct monad. We need to translate each morphism into a common coproduct monad. For example in the following program, we need to convert each error from each stage into a common error type such that every morphism lives in the same monad.
lexE : List Char -> Either LexerError (List Token)
parseE : List Token -> Either ParseError Tree
typecheckE : Tree -> Either TypeError Sema
data CompilerErr
= LexE LexerError
| ParseE ParseError
| TypeE TypeError
runCompilerErr : Kleislimorphism (Either CompilerErr) String Bytecode
runCompilerErr =
RunCat Type (Kleislimorphism (Either CompilerErr)) CompilerPipeline
[Kleisli (pure . unpack),
Kleisli (mapFst LexE . lexE),
Kleisli (mapFst ParseE . parseE),
Kleisli (mapFst TypeE . typecheckE),
Kleisli (pure . codegen)]
While writing mapFst with the appropriate error-conversion function is not the end of the world,
it feels like something we should be able to deal with automatically. This is the topic of the next
section.
Abstracting to graded categories
To ease the handling of errors, we are going to further generalise our pipelines to graded categories. A graded category is like a category but carries an additional monoid that will annotate each morphism. We define graded categories as :
- A set of objects $C$.
- A monoid $G$.
- For all $x, y \in C$ and $g \in G$ we have a set of graded morphisms
x -[g]> y. - An identity morphism
x -[u]> xwhereuis the monoidal unit in $G$. - Graded morphism composition
x -[g]> y,y -[h]> ztox -[g <+> h]> zwhere<+>is the multiplication of the monoid. - And the usual proofs of associativity and identity.
We can implement graded categories as an interface, and ignore the proofs for simplicity.
export infixr 1 #>
public export
interface GradedCat (mon : Monoid gr) (0 arr : gr -> obj -> obj -> Type) | arr where
constructor MkGradedCat
identity : forall x. arr (Prelude.Interfaces.neutral @{mon}) x x
(#>) : forall x, y, z. {g1, g2 : _} -> arr g1 x y -> arr g2 y z -> arr (g1 <+> g2) x z
With this approach, we can write a graded pipeline where we first give a list of layers for it, then additionally, we provide a list of morphisms and a list of grades for each morphism.
-- We parameterise everything by
-- the grade, the objects and the graded morphisms
parameters (0 gr : Type) (0 obj : Type) (0 arr : gr -> obj -> obj -> Type)
-- An implementation needs both the layers of the pipeline, and the grades of each morphism.
-- For each triple of `source`, `target` and `grade` we build the graded morphism `source -[grade]> target`
-- as the type of the implementation of the corresponding stage
ImplGr : forall n. Vect (2 + n) obj -> Vect (S n) gr -> Type
ImplGr layers grades = All (\arg => arr (fst arg) (fst (snd arg)) (snd (snd arg))) (zip grades (pairUp layers))
This way, given a list of layers [a, b, c, d] and a list of grades [g1, g2, g3] we obtain a list of graded morphisms [a -[g1]> b, b -[g2]> c, c -[g3]> d.
To run this list of morphisms we compose each of them using graded morphism composition: because we have a list of grades [g1, g2, g3] the resulting morphism will have the grade g1 <+> g2 <+> g3. The final morphism will have type a -[g1 <+> g2 <+> g3]> d.
RunGrCat : forall n. (mon : Monoid gr) => (cat : GradedCat mon arr) ->
(p : Vect (2 + n) obj) -> (grades : Vect (S n) gr) ->
ImplGr p grades -> arr (foldGrades grades) (Vect.head p) (Vect.last p)
RunGrCat cat [x, y] [gr] [f] = f
RunGrCat cat (x :: y :: z :: xs) (gr1 :: (g :: gs)) (f :: c :: cs) =
f #> RunGrCat cat (y :: z :: xs) (g :: gs) (c :: cs)
Implementing errors with Either
With this infrastructure, we can build the graded pipeline of compiler stages with errors.
Whenever a stage returns no error we use Either Void to indicate that the Left choice is
impossible. First we need to define an appropriate monoid, in this case, we want a monoid on Type where each value represent a possible error, we combine them with Either to say that only one of the two possible given errors is going to occur
[CoprodSemi] Semigroup Type where
(<+>) = Either
[CoprodMon] Monoid Type using CoprodSemi where
neutral = Void
GradedEither : Type -> Type -> Type -> Type
GradedEither g a b = a -> Either g b
With this monoid, we define the graded category where morphisms are graded kleisli arrows a -> Either g b
[EitherGrCat] GradedCat CoprodMon GradedEither using CoprodSemi where
identity = pure
(#>) f g x =
case f x of
Left err => Left (Left err)
Right v =>
case g v of
Left err => Left (Right err)
Right v => pure v
Finally, we implement a compiler with errors by using our monoid on types and our graded category. The implementation is as expected and the types compose automatically.
lexErr : List Char -> Either LexerError (List Token)
parseErr : List Token -> Either ParseError Tree
typecheckErr : Tree -> Either TypeError Sema
CompilerEither : String -> Either ? Bytecode
CompilerEither = RunGrCat @{CoprodMon} Type Type (\g, x, y => x -> Either g y)
EitherGrCat CompilerPipeline [Void, LexerError, ParseError, TypeError, Void]
[pure . unpack, lexErr, parseErr, typecheckErr, pure . codegen]
The full type of this function is quite large, and contains some redundancy with Either Void:
CompilerEither : String -> Either (Either Void (Either LexerError (Either ParseError (Either TypeError Void)))) Bytecode
While we managed to handle errors automatically, it would be nice if our implementation did not suffer from those artefacts. Thankfully, this is easily done by changing the monoid we are working with.
Implementing errors with Any
To address the problem of redundant neutral values from the previous example, we use the List monoid rather than
Type and Either. With [] as the neutral element and concatenation (++) as the monoidal operations, lists
naturally ignore their neutral elements when combined. A program that returns no error therefore returns an
empty list of errors, and programs with errors return a singleton list containing the error they emit.
Now that we know that we want to grade our arrows by lists, we have yet to define what is an appropriate morphism
graded by such a list. For this we use the OneOf : List Type -> Type type, a sort of iterated coproduct where each
possible choice is given by the types in the list. We write it as a special case of Any: a predicate on lists
asserting that exactly one element in a list of a fullfils the predicate p : a -> Type.
data Any : (p : a -> Type) -> List a -> Type where
Here : {0 p : a -> Type} -> p x -> Any p (x :: xs)
There : Any p xs -> Any p (x :: xs)
OneOf : List Type -> Type
OneOf = Any id
Using OneOf we define a graded category where the monoid is given by List and the morphisms by functions
a -> Either (OneOf g) b. We write them as a -[g]> b.
GrListMor : List Type -> Type -> Type -> Type
GrListMor g x y = x -> Either (OneOf g) y
[OneOfCat] GradedCat %search GrListMor where
-- Elided for brevity
Using some idris notation trickery and this graded category, we can define our list of compiler stages with grades where some stages do not emit any errors and some have their own bespoke errors.
namespace GradedCompilerAny
split : String -[]> List Char
lex : List Char -[LexerError]> List Token
parse : List Token -[ParseError]> Tree
typecheck : Tree -[TypeError]> Sema
codegen : Sema -[]> Bytecode
CompilerErrors : Vect 5 (List Type)
CompilerErrors = [[], [LexerError], [ParseError], [TypeError], []]
runGradedCompiler : String -[LexerError, ParseError, TypeError]> Bytecode
runGradedCompiler = RunGrCat (List Type) Type (\g, a, b => a -> Either (OneOf g) b)
OneOfCat CompilerPipeline CompilerErrors
[split, lex, parse, typecheck, codegen]
The result is an elegant function String -[LexerError, ParseError, TypeError]> Bytecode containing
only the errors we care about and the implementation is essentially the same as the version using
Either.
Conclusion
The same pipeline architecture can run all sorts of programs by generalising to categories. The pattern works not only for pure and monadic programs, but also for lenses and dependent lenses. Generalising further to graded categories yields a way to dynamically combine errors without additional ceremony. Although we haven’t had the time to talk about it here, the ability to use graded morphisms also comes in handy for composing graded dependent lenses which we can obtain via the para-construction on dependent lenses for example.