In this post I’ll describe the theory of how to add iteration to categories of optics. Iteration is required for almost all applications of categorical cybernetics beyond game theory, and is something we’ve been handling only semi-formally for some time. The only tool we need is already one we have inside the categorical cybernetics framework: parametrisation weighted by a lax monoidal functor. I’ll end with a conjecture that this is an instance of a general procedure to force states in a symmetric monoidal category.

This post is strongly inspired by the account of Moore machines in David Jaz Myers’ book Categorical Systems Theory, and Matteo’s enthusiasm for it. There’s probably a big connection to things like Delayed trace categories, but I don’t understand it yet.

The diagrams in this post are made with Quiver and Tangle.

The iteration functor

For the purposes of this post, we’ll be working with a symmetric monoidal category $\mathcal C$, and the category $\mathbf{Optic} (\mathcal C)$ of monoidal optics over it. Objects of $\mathbf{Optic} (\mathcal C)$ are pairs of objects of $\mathcal C$, and morphisms are given by the coend formula

which amounts to saying that an optic $\binom{X}{X’} \to \binom{Y}{Y’}$ is an equivalence class of triples

I’m pretty sure everything in this post works for other categories of bidirectional processes such as mixed optics and dependent lenses, this is just a setting to write it down which is both convenient and not at all obvious.

The iteration functor is a functor $\mathrm{Iter} : \mathbf{Optic} (\mathcal C) \to \mathbf{Set}$ defined on objects by

We refer to elements of $\mathrm{Iter} \binom{X}{X’}$ as iteration data for $\binom{X}{X’}$. We call the object $M$ the state space, the morphism $x_0 : I \to M \otimes X$ the initial state and the morphism $i : M \otimes X’ \to M \otimes X$ the iterator.

Note that in the common case that $\mathcal C$ is cartesian monoidal, we can eliminate the coend to obtain a simpler characterisation:

Given an optic $f : \binom{X}{X’} \to \binom{Y}{Y’}$ given by $f = (N, f : X \to N \otimes Y, f’ : N \otimes Y’ \to X’)$, we get a function

Namely, the state space is $M \otimes N$, the initial state is

and the iterator is

This is evidently functorial. Funnily enough, although the action of $\mathrm{Iter}$ on objects when $\mathcal C$ is cartesian is easier to understand, its action on morphisms is less obvious and is not evidently functorial, instead demanding a small proof.

Pairing iterators and continuations

We have an existing functor $K : \mathbf{Optic} (\mathcal C)^{\mathrm{op}} \to \mathbf{Set}$, given on objects by $K \binom{X}{X’} = \mathcal C (X, X’)$. This is the continuation functor, and it is the contravariant functor represented by the monoidal unit $\binom{I}{I}$. (This functor first appeared in Morphisms of Open Games.)

For the remainder of this section I’ll specialise to the case $\mathcal C = \mathbf{Set}$, in which case an optic $\binom{X}{X’} \to \binom{Y}{Y’}$ is determined by a pair of functions $f : X \to Y$ and $f’ : X \times Y’ \to X’$, and iteration data $i : \mathrm{Iter} \binom{X}{X’}$ is determined by an initial value $x_0 : X$ and a function $i : X’ \to X$.

Given iteration data and a continuation that agree on their common boundary, we know enough to run the iteration and produce an infinite stream of values:

Namely, this stream is defined corecursively by

This operation is natural (technically, dinatural): for any iteration data $i : \mathrm{Iter} \binom{X}{X’}$, optic $f : \binom{X}{X’} \to \binom{Y}{Y’}$ and continuation $k : K \binom{Y}{Y’}$, we have

where $f^\omega (-) : X^\omega \to Y^\omega$ means applying the forwards pass of $f$ to every element of the stream. As a commuting diagram,

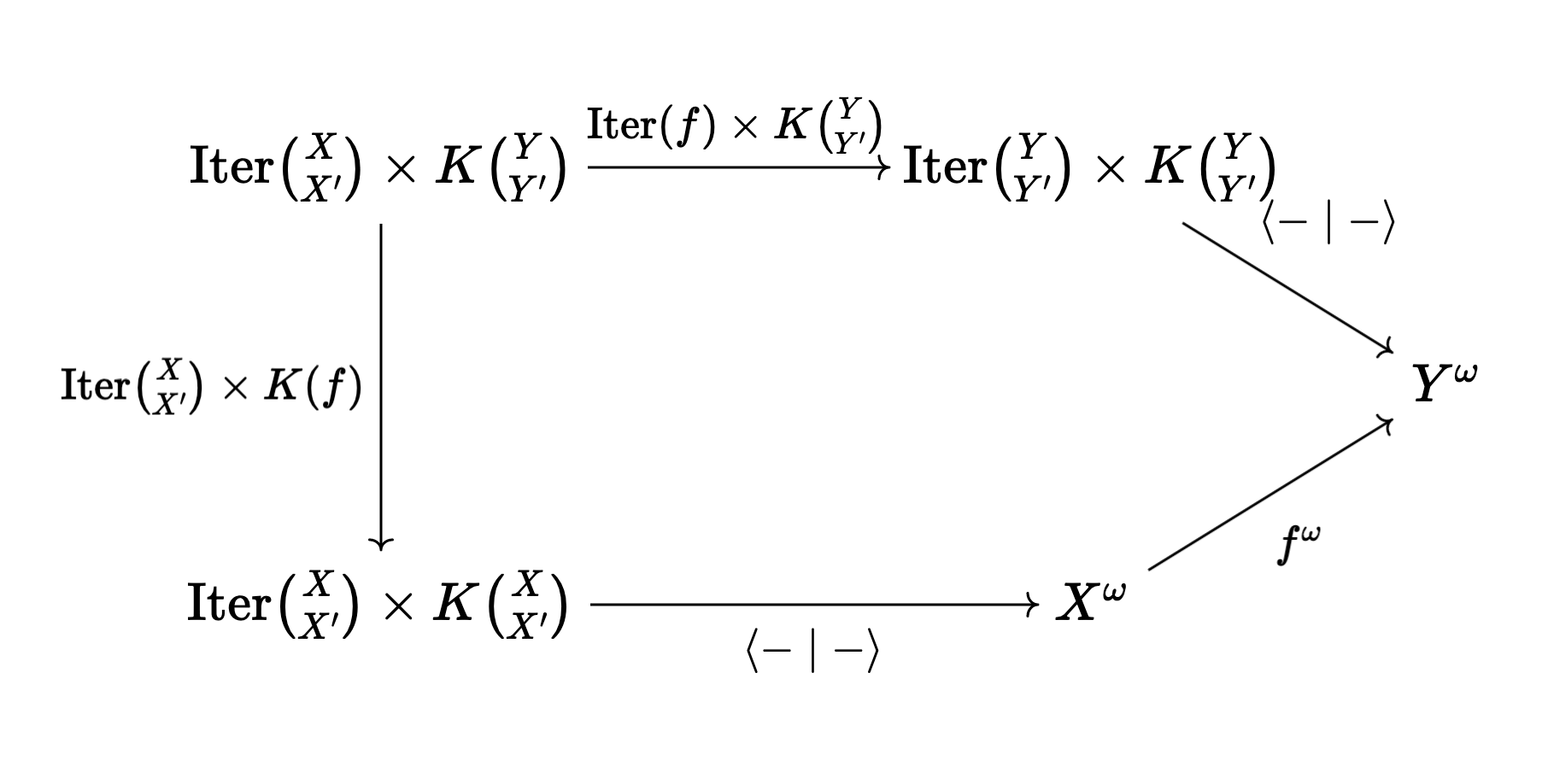
Here’s a tiny implementation of the iteration functor and the pairing operator in Haskell:

data Iterator s t = Iterator {
    initialState :: s,
    updateState :: t -> s
}

mapIterator :: Lens s t a b -> Iterator s t -> Iterator a b
mapIterator l (Iterator s f) = Iterator (s ^# l) (\b -> (f (s & l .~ b)) ^# l)

runIterator :: Iterator s t -> Lens s t () () -> [s]
runIterator (Iterator s f) l = s : runIterator (Iterator (f (s & l .~ ())) f ) l

The category of elements of Iterator

The next step is to form the category of elements $\int \mathrm{Iter}$, also known as the discrete Grothendieck construction. This is a category whose objects are tuples $\left( \binom{X}{X’}, i \right)$ of an object $\binom{X}{X’}$ of $\mathbf{Optic} (\mathcal C)$ and a choice of iteration data $i : \mathrm{Iter} \binom{X}{X’}$. A morphism $\left( \binom{X}{X’}, i \right) \to \left( \binom{Y}{Y’}, j \right)$ is an optic $f : \binom{X}{X’} \to \binom{Y}{Y’}$ with the property that $\mathrm{Iter} (f) (i) = j$, that is to say, the iteration data on the left and right boundary have to agree.

The functor $\mathrm{Iter} : \mathbf{Optic} (\mathcal C) \to \mathbf{Set}$ is lax monoidal: there is an evident natural way to combine pairs of iteration data into iteration data for pairs:

This means that the tensor product of $\mathbf{Optic} (\mathcal C)$ lifts to $\int \mathrm{Iter}$, by

The category $\int \mathrm{Iter}$ can essentially already describe iteration with optics, although in a slightly awkward way. Suppose we draw a string diagram that not coincidentally resembles a control loop:

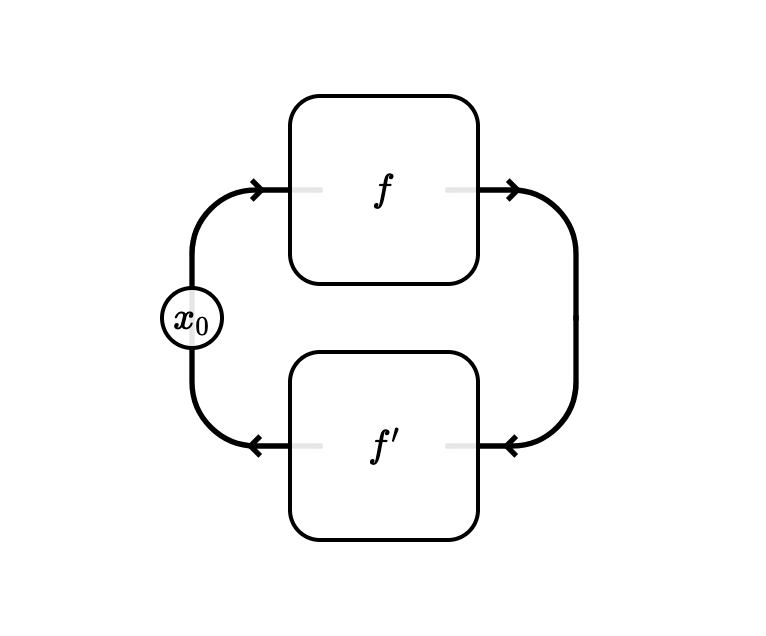
Here, $f$ and $f’$ denote some morphisms $f : X \to Y$ and $f’ : Y \to X$ in our underlying category, and $x_0$ represents an initial state $x_0 : I \to X$.

Normally string diagrams denote morphisms of a monoidal category, but we make a cut just to the right of the backwards-to-forwards turning point, and consider that everything left of that is describing a boundary object. Namely in this case, we have the object $\left( \binom{X}{X}, i \right)$ where the iteration data $i : \mathrm{Iter} \binom{X}{X}$ is given by the state space $I$, the initial state $x_0 : I \to I \otimes X$ and the iterator $\mathrm{id} : I \otimes X \to I \otimes X$.

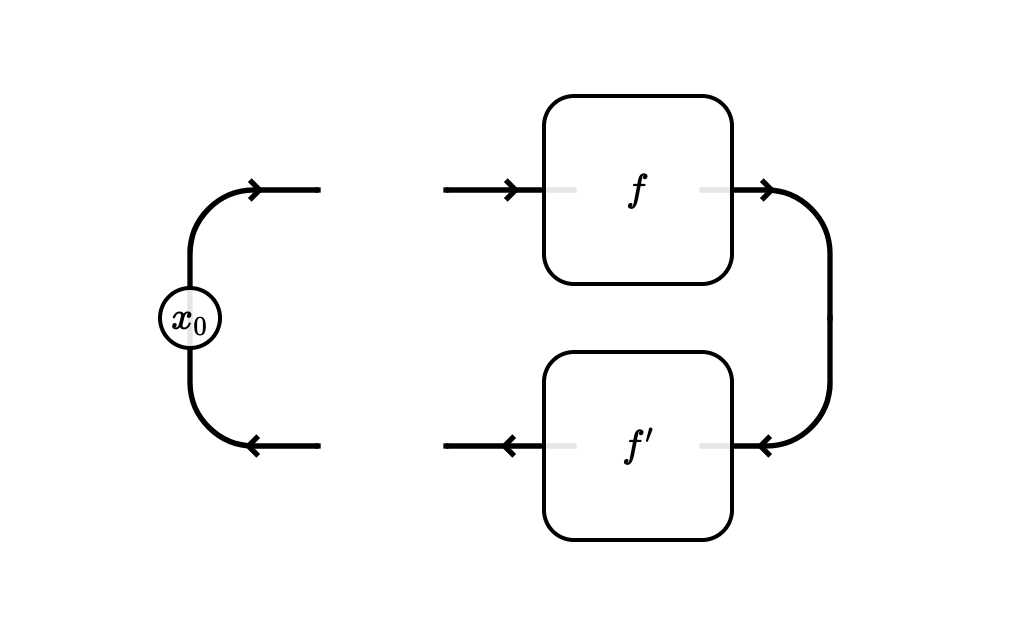
The remainder of the string diagram to the right of the cut denotes an ordinary optic $f : \binom{X}{X} \to \binom{I}{I}$, namely the one given by $f = (Y, f, f’)$, with forwards pass $f : X \to Y \otimes I$ and backwards pass $f’ : Y \otimes I \to X$. This boils down to describing the composite morphism $f; f’ : X \to X$.

Overall, we can read this diagram as denoting a morphism $f$ in $\int \mathrm{Iter}$ of type $f : \left( \binom{X}{X}, i \right) \to \left( \binom{I}{I}, \mathrm{Iter} (f) (i) \right)$. The iteration data on the right boundary is $\mathrm{Iter} (f) (i) : \mathrm{Iter} \binom{I}{I}$, which concretely has state space $Y$, the initial state $x_0; f : I \to Y$ and iterator $f’; f : Y \to Y$.

This works in principle, but splitting the diagram between denoting an object and denoting a morphism is very non-standard. So far, this amounts to doing for the iteration functor what we did for the selection functions functor in section 6 of Towards Foundations of Categorical Cybernetics.

The full theory of iteration

Now we take the final step to fix the slight clunkiness of using $\int \mathrm{Iter}$ as a model of iteration. This continues the firmly established pattern that categorical cybernetics contains only two ideas that get combined in more and more intricate ways: optics and parametrisation.

There is a strong monoidal functor $\pi : \int \mathrm{Iter} \to \mathbf{Optic} (\mathcal C)$ that forgets the iteration data, namely the discrete fibration $\pi \left( \binom{X}{X’}, i \right) = \binom{X}{X’}$. This functor generates an action of the monoidal category $\int \mathrm{Iter}$ on $\mathbf{Optic} (\mathcal C)$, namely

See section 5.5 of Actegories for the Working Amthematician for far too much information about actegories of this form.

We now take the category $\mathbf{Para}_{\int \mathrm{Iter}} (\mathbf{Optic} (\mathcal C))$ of parametrised morphisms generated by this action. We also refer to this kind of thing (parametrisation for the action generated by a discrete fibration) as the Para construction weighted by $\mathrm{Iter}$, $\mathbf{Para}^\mathrm{Iter} (\mathbf{Optic} (\mathcal C))$ - the name comes from it being a kind of weighted limit and I think the reference for this is Bruno’s PhD thesis, which is sadly unreleased as I’m writing this.

Working things through: an object of $\mathbf{Para}^\mathrm{Iter} (\mathbf{Optic} (\mathcal C))$ is still a pair $\binom{X}{X’}$, but a morphism $\binom{X}{X’} \to \binom{Y}{Y’}$ consists of three things: another pair of objects $\binom{Z}{Z’}$, iteration data $i : \mathrm{Iter} \binom{Z}{Z’}$, and an optic $\binom{X \otimes Z}{X’ \otimes Z’} \to \binom{Y}{Y’}$.

Now suppose we have a diagram of an open control loop, that is to say, a control loop that is open-as-in-systems (not to be confused with an open loop controller, which is unrelated):

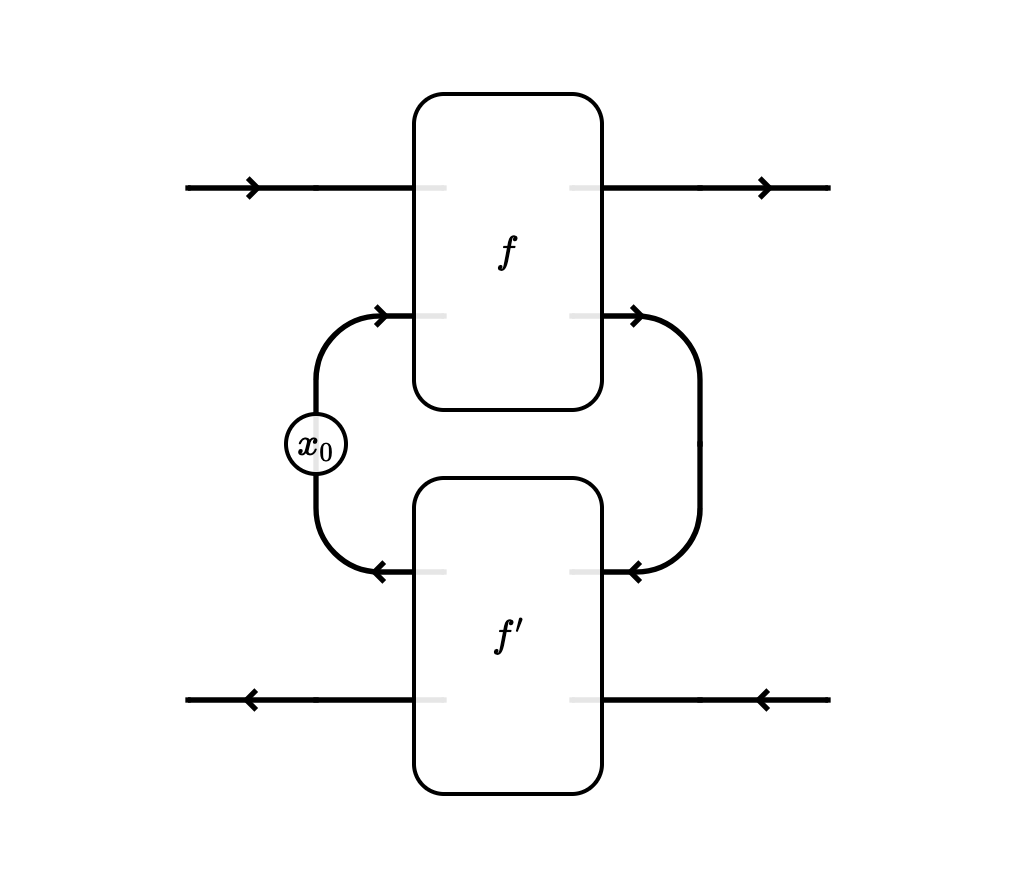
Here the primitive morphisms in the diagram are $f : A \otimes X \to B \otimes Y$, $f’ : B’ \otimes Y \to A’ \otimes X$, and an initial state $x_0 : I \to X$. The idea is that $f$ is the forwards pass, $f’$ is the backwards pass, and after the backwards pass comes another forwards pass but one time step in the future.

To make formal sense of this diagram, we imagine that we deform the backwards-to-forwards bend upwards, treating the state as a parameter, and then cut the diagram as we did before:

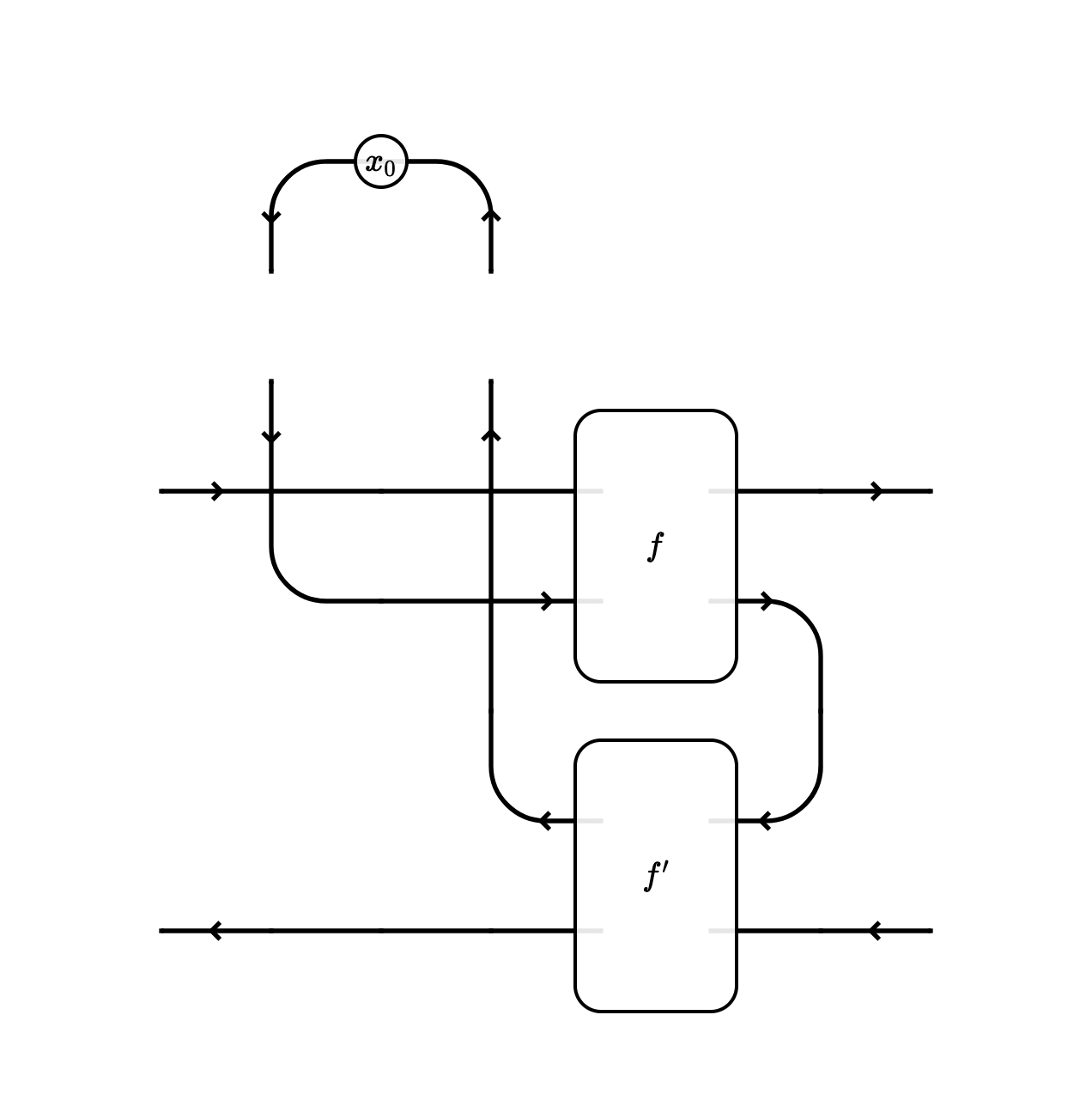
Now we can read this off as a morphism $\binom{X}{X’} \to \binom{Y}{Y’}$ in $\mathbf{Para}^\mathrm{Iter} (\mathbf{Optic} (\mathcal C))$. The (weighted) Para construction makes everything go smoothly, so this is an entirely standard string diagram with no funny stuff.

Technically categories of parametrised morphisms are always bicategories (or better, double categories), and I think this is a rare case where we actually want to quotient out all morphisms in the vertical direction, i.e. identify $\left( f : \binom{X \otimes Z}{X’ \otimes Z’} \to \binom{Y}{Y’}, i : \mathrm{Iter} \binom{Z}{Z’} \right)$ with $\left( g : \binom{X \otimes W}{X’ \otimes W’} \to \binom{Y}{Y’}, j : \mathrm{Iter} \binom{W}{W’} \right)$ whenever there is any optic $h : \binom{Z}{Z’} \to \binom{W}{W’}$ making $\mathrm{Iter} (h) (i) = j$ and commuting with $f$ and $g$. Coming back to our earlier picture of cutting a string diagram, this exactly says that we identify all of the different ways we could make the cut. In order to do this we change the base of enrichment along the functor $\pi_0 : \mathbf{Cat} \to \mathbf{Set}$ taking each category to its set of connected components.

One final note: Almost everything in this post used nothing but the fact that $\mathrm{Iter}$ is a lax monoidal functor $\mathbf{Optic} (\mathcal C) \to \mathbf{Set}$. With minimal translation, I think the entire thing works as a story about “forcing states in a symmetric monoidal category”: given any symmetric monoidal category $\mathcal C$ and a lax monoidal functor $F : \mathcal C \to \mathbf{Set}$, the category $\mathbf{Para}^F (\mathcal C)$ is equivalently described as $\mathcal C$ freely extended with a morphism $x : I \to X$ for every $x : F (X)$. I’ll leave this as a conjecture for somebody else to prove.